|
Probabilités
et statistiques
La partie du programme consacrée aux
probabilités et à la statistique est centrée:
- sur la mise en place d’éléments de base
indispensables pour comprendre ou pratiquer la statistique partout où elle
est présente,
- sur l’acquisition de concepts de probabilité
permettant de comprendre et d’expliquer certains faits simples observés
expérimentalement ou par simulation.
Le programme de la classe de première introduit quelques
outils
descriptifs nouveaux:
·
les
diagrammes en boîtes qui permettent d’appréhender aisément certaines
caractéristiques des répartitions des caractères étudiés et qui
complètent la panoplie des outils graphiques les
plus classiquement utilisés;
·
deux
mesures de dispersion: l’écart-type et l’intervalle interquartile.
Ces éléments de statistique pourront notamment
être travaillés pour des séries construites à partir de séries simulées; on
rencontre ainsi des répartitions variées et on prépare la notion
d’estimateur.
Statistique
Variance et écart type.
Diagramme en boîtes et intervalle interquartile
. Influence sur l’écart type et l’intervalle interquartile d’une
transformation affine des données.
On cherchera
des résumés pertinents et on commentera les diagrammes en boîtes de
quantités numériques associées à des séries simulées ou non .
On observera l’influence des valeurs extrêmes d’une série sur l’écart type
ainsi que la fluctuation de l’écart type entre séries de même taille.
L’usage d’un tableur ou d’une calculatrice permettent d’observer
dynamiquement et en temps réel , les effets des modifications des données.
L’objectif est de résumer une série par un couple (mesure de
tendance centrale ; mesure de dispersion) . Deux choix usuels sont
couramment proposés : le couple (médiane ; intervalle
interquartile) , robuste par rapport aux
valeurs extrêmes de la série et le (couple moyenne ; écart type). On
démontrera que la moyenne est le réel qui minimise
å
(xi-x)2 , alors qu’elle ne minimise pas
å
½xi-x½
On notera s l’écart type d’une série plutôt que
s ,
réservé à l’écart type d’une loi de probabilité.
Probabilités
Définition d’une loi de probabilité sur un
ensemble fini . Espérance , variance , écart type d’une loi de probabilité .
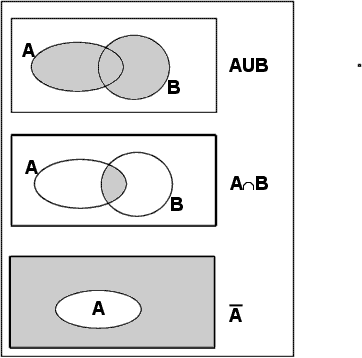
Probabilité d’un événement , de la réunion et de l’intersection
d’événements. Cas de l’équiprobabilité .
Variable aléatoire , loi d’une variable
aléatoire, espérance , variance , écart type .
Modélisation d’expériences aléatoires de
référence
(lancers d’un ou plusieurs dés ou pièces
discernables ou non , tirage au hasard dans une urne , choix de chiffres au
hasard , etc ..)
Le lien entre loi de probabilité et distributions de fréquences sera
éclairé par un énoncé vulgarisé de la loi des grands nombres . On expliquera
ainsi la convergence des moyennes vers l’espérance et des variances
empiriques vers les variances théoriques ; on illustrera ceci par des
simulations dans des cas simples . On pourra aussi illustrer cette loi avec
les diagrammes en boîtes obtenus en simulant par exemple 100 sondages de
taille n pour n=10 ; 100 ; 1000.
On simulera des lois de probabilités simples comme images d’une loi
équirépartie par une variable aléatoire ( sondage , somme des faces de deux
dés, etc…)
On
pourra par exemple choisir comme énoncé vulgarisé de la loi des grands
nombres la proposition suivante :
Pour une expérience donnée , dans le modèle
défini par une loi de probabilité P , les distributions des fréquences
calculées sur des séries de taille n se rapprochent de P quand n devient
très grand .
On
indiquera que simuler une expérience consiste à simuler un modèle de cette
expérience .La modélisation avec des lois ne découlant pas d’une loi
équirépartie est hors programme .
On évitera le calcul systématique et sans but précis de
l’espérance et de la variance de lois de probabilité. |
Statistique
et probabilité (Page 67 )
En classe de
seconde, les élèves ont été sensibilisés à la fluctuation d’échantillonnage
dans des cas simples correspondant à des expériences aléatoires dont le
résultat ne peut prendre qu’un nombre fini de valeurs ; ils ont fait et
simulé des expériences liées à des choix de chiffres au hasard : ces
expériences et ces simulations ont en principe été consignées dans un
cahier de statistique (dans de tels cahiers, les élèves ont écrit
pourquoi telle expérience est faite, ce que l’on observe, des explications
éventuelles de ce qui est observé, et fait le lien entre diverses
expériences et simulations).
Le programme
de Probabilités-Statistique de la série S introduit les notions de
loi de probabilité et de variable aléatoire, notions indispensables pour
comprendre l’esprit de la statistique et aborder la
problématique propre à cette discipline ; quelques éléments de
statistique descriptive sont introduits, mais celle-ci a une part modeste
dans cette série.
La
terminologie en usage pour la statistique et les probabilités sera réduite
au minimum;
L’important
est de savoir résoudre des problèmes, de relier les résultats de calculs
faits sur des observations aux questions posées.
On trouvera
en fin de cette annexe un lexique des principaux termes liés à
la statistique et que l’élève doit connaître.
Lexique
pages 73 et 74
Définition de la médiane dans le
lexique
Statistique
descriptive
( pages 67 et
68,)
Quelques
éléments de statistique descriptive sont présentés pour les séries
numériques :écart type et diagramme en boîte (cf. annexe commune aux
séries ES, L et S, p. 83).
Il est
important ici de démontrer que la moyenne minimise la fonction
x S (xi –x )2 qui mesure la dispersion autour d’un
point, et que ce minimum est appelé variance.
Les
diagrammes en boîte permettent une comparaison graphique de plusieurs séries
de données
(voir fiche «Sondages» du document d’accompagnement de seconde) ; on
remarquera à l’aide d’exemples que le résumé d’une série par le couple
(médiane, écart interquartile) n’est pas sensible aux valeurs extrêmes et ne
peut faire l’objet de calculs par paquets. Résumer une série de données par
moyenne, écart type a des propriétés théoriques qui rendent son usage
fréquent, notamment en biologie et physique pour ce qui touche aux mesures
expérimentales
On notera que
la moyenne d’une série de données étant l’isobarycentre des
termes et le barycentre des valeurs prises pondérées par les fréquences,
elle bénéficie de la propriété d’associativité des barycentres et permet
donc les calculs par sous-groupes.
Un recueil
effectif de données par les élèves n’est à envisager que s’il ne prend pas
beaucoup de temps et traite d’une question que les élèves ont fortement
contribué à formuler.
L’objectif
reste toujours de savoir quelle question ou étude a motivé de traiter des
données, de comprendre les calculs et de savoir interpréter les résultats.
Annexe boîtes et quantiles pages 85 à
88
Exemples de
diagrammes en boîtes.
Probabilité ,
modélisation , simulation
( pages 68 à 72 )
Loi de
probabilité (
pages 68 et 69 )
les élèves
devront bien distinguer ce qui est empirique (fréquence ) de ce qui est
théorique
(probabilité
).
Si tous les
éléments d’un ensemble ont même probabilité , la loi de probabilité est dite
équirépartie .
On évitera
tout développement théorique sur le langage des événements et le calcul
ensembliste qui en découle .
Exercices page 70
Variable
aléatoire
( pages 69 et 70)
définie
comme une application qui permet de transformer une loi de probabilité en
une autre loi de probabilité .
Elle ne
conserve pas en général l’équiprobabilité .
Espérance ,
variance et écart type d’une loi de probabilité ou d’une variable
aléatoire : c’est la même notion .
Linéarité
non évoquée dans le programme : son utilisation possible s’appuiera sur les
statistiques .
Exemple 2 page 48 :
somme de deux dés
Modélisation (
pages 70 et 71 ):
Modéliser une
expérience aléatoire , c’est associer à cette expérience un ensemble et une
loi de probabilité sur cet ensemble .
On se
limitera aux expériences de référence.
Pour valider
un modèle probabiliste , le premier outil dont on dispose est la loi forte
des grands nombres
Simulation de
chiffres au hasard
( pages 72 et
73 )
|